Ensembles de Mandelbrot et de Julia (version simplifiée)
lundi 21 juillet 2025
1 – Ensembles de Julia
On considère une fonction \(f\) à valeurs complexes, définie sur \(\mathbf{C}\) (privé d'éventuellement quelques points), et on l'utilise pour former des suites \((u_n)_{n \geq 0}\) avec la relation de récurrence \[ u_{n + 1} = f(u_n). \] On suppose qu'il y a un nombre \(d\) au moins égal à deux tel que \[ f(z) \underset{\infty}{=} z^d \times \left(1 + O\!\left(\frac{1}{z}\right)\right), \] par exemple \(f\) pourrait être un polynôme unitaire de degré \(d\), ou une fraction rationnelle formée du quotient de deux polynômes unitaires dans laquelle le degré du numérateur excède d'au moins deux unités celui du dénominateur. Pour les suites fabriquées à partir de ces fonctions, l'infini est un point attracteur : il y a un « disque » autour de \(\infty\) dans lequel si la suite entre, alors elle diverge vers l'infini. Voilà comment on dit ça plus précisément :Propriété (l'infini est un point attracteur).
Soit \(f\) et \((u_n)_{n \geq 0}\) comme ci-dessus. Il y a un nombre \({\tt R\_MAX}\), et s'il existe un indice \(n\) pour lequel \(|u_n| \geq {\tt R\_MAX}\), alors \(|u_n| \underset{n\infty}{\longrightarrow} +\infty\).
Preuve. Puisque \(f(z) \underset{\infty}{=} z^d \times (1 + O(1/z))\) on a aussi \(|f(z)| \underset{\infty}{=} |z|^d \times |1 + O(1/z)|\) et puisque \(1/z\) tend vers zéro on peut trouver un nombre \({\tt R\_MAX}\) (et ce ne sont pas des baskets : je la place ici discrètement) tel que pour \(|z| \geq {\tt R\_MAX}\) on a
\[ |f(z)| \geq |z|^d \times \left(1 - \frac{1}{2}\right) = \frac{|z|^d}{2}. \]
Supposons alors que pour un certain indice \(n\) on a \(|u_n| \geq {\tt R\_MAX}\). Alors
\[ |u_{n + 1}| = |f(u_n)| \geq \frac{|u_n|^d}{2} \geq \frac{{\tt R\_MAX}^d}{2}. \]
Quite à l'augmenter un brin, on peut supposer que \({\tt R\_MAX}\) est au moins égal à \(2\), de sorte que
\[ \frac{{\tt R\_MAX}^d}{2} \geq \frac{{\tt R\_MAX}^{d - 1} \times 2}{2} = {\tt R\_MAX}^{d - 1} \geq {\tt R\_MAX} \]
(puisque, rappelons-le, \(d\) est au moins égal à deux). Ainsi \(|u_{n + 1}| \geq {\tt R\_MAX}\) et on peut maintenant effectuer deux raisonnements par récurrence. Le premier pour voir que \(|u_{n + k}| \geq {\tt R\_MAX}\) pour tout indice \(k\), et donc (en appliquant ce qu'on sait sur \(f\)) que
\[ |u_{n + k + 1}| = |f(u_{n + k})| \geq \frac{|u_{n + k}|^d}{2} \]
toujours pour tout indice \(k\). En multipliant astucieusement les deux membres ci-dessus par \(2^{1/(1 - d)}\) on obtient
\[ 2^{\frac{1}{1 - d}} \times |u_{n + k + 1}| \geq 2^{\frac{1}{1 - d} - 1} \times |u_{n + k}|^d = 2^{\frac{d}{1 - d}} \times |u_{n + k}|^d = \left(2^{\frac{1}{1 - d}} \times |u_{n + k}|\right)^{\!d}. \]
Un second raisonnement par récurrence montre alors que
\[ 2^{\frac{1}{1 - d}} \times |u_{n + k}| \geq \left(2^{\frac{1}{1 - d}} \times |u_{n}|\right)^{\!d^k} \quad\quad\text{ou encore}\quad\quad |u_{n + k}| \geq 2^{\frac{1}{d - 1}} \times \left(2^{\frac{1}{1 - d}} \times |u_{n}|\right)^{\!d^k}. \]
Ça paraît compliqué, mais comme \(2^{\frac{1}{1 - d}}\) est l'inverse de \(\sqrt[d-1]{2}\), et qu'on a dit \(|u_n| \geq {\tt R\_MAX} \geq 2\), le nombre dans la grande parenthèse ci-dessus est plus grand que \(1\) et on a donc \(|u_{n+k}| \underset{k\infty}{\longrightarrow} +\infty\). C.Q.F.D.
Pour simplifier on prend un nombre très grand qui convient « à tous les coups », ce qui évidemment suppose qu'on n'utilisera pas une fonction \(f\) trop originale.
R_MAX = 1.0e+100
R_MAX_CARRÉ = 1.0e+200
L'observation faite n'est pas banale : soit la suite \((u_n)_{n \geq 0}\) est bornée, soit elle diverge vers l'infini, sans aucune alternative (alors qu'en général il y a évidemment beaucoup d'autres situations envisageables). L'ensemble de Julia « rempli » de \(f\) est celui des valeurs initiales \(u_0\) pour lesquelles la suite est bornée : \[ \mathscr{J}_{\mathrm{rempli}}(f) = \left\{ u_0 \;\middle|\; |u_n| \underset{n\infty}{\nrightarrow} +\infty \right\}. \] L'itération de Julia consiste à chercher à partir de quel indice \(n\) on entre dans ce disque autour de \(\infty\). Évidemment si la suite est bornée on n'y entre jamais, il faut donc prévoir un nombre maximal d'itérations à tester. On renvoie le couple \((n, u_n)\) correspondant. Attention, lorsque c'est la condition \(n = {\tt N\_MAX}\) qui met fin à la boucle, on n'a pas forcément \(|u_n| \geq {\tt R\_MAX}\).
N_MAX = 50
def ItérationDeJulia(f, u_0) :
z = u_0 ; n = 0
# à chaque instant on aura z = u_n
while n < N_MAX and abs(z) < R_MAX :
z = f(z)
n += 1
return (n, z)
Pour dessiner l'ensemble \(\mathscr{J}_{\mathrm{rempli}}(f)\), on regarde tous les pixels dans le fenêtrage choisi, et on utilise un dégradé comme on l'a vu précédemment pour colorier chacun d'eux en fonction de l'indice \(n\) pour lequel on entre dans le disque autour de l'infini.
# Dessin de l'ensemble de Julia fermé pour une fonction f
def Julia(f, d, Palette) :
I = CréerDessin(LARGEUR, HAUTEUR)
for px in range(LARGEUR) :
for py in range(HAUTEUR) :
(x, y) = PixelVersPoint(px, py)
(n, u_n) = ItérationDeJulia(f, x + y * 1j)
Couleur = Palette[int(n / N_MAX * (len(Palette) - 1))]
I.putpixel( (px, py), Couleur )
Afficher(I)
Essayons.
>>> Centrer(0.0, 0.0, 2.0)
>>> N_MAX = 50
>>> ROUGE = (255, 110, 90)
>>> P = ConstruirePaletteDégradéSimple(100, ROUGE)
>>> Julia(lambda z : z ** 2 + 1.0j, Palette = P)

2 – Vitesse de divergence
>>> Centrer(0.0, 0.0, 2.0)>>> N_MAX = 250
>>> NOIR = (0, 0, 0) ; OUTREMER = (10, 40, 128) ; BLEU = (130, 170, 255) ; CYAN = (0, 255, 255) ; BLANC = (255, 255, 255)
>>> P = ConstruirePaletteDégradéMultiple(100, [NOIR, BLEU, OUTREMER, CYAN])
>>> Julia_lisse(lambda z : z ** 2 + 0.285 + 0.01j, d = 2, Palette = P)
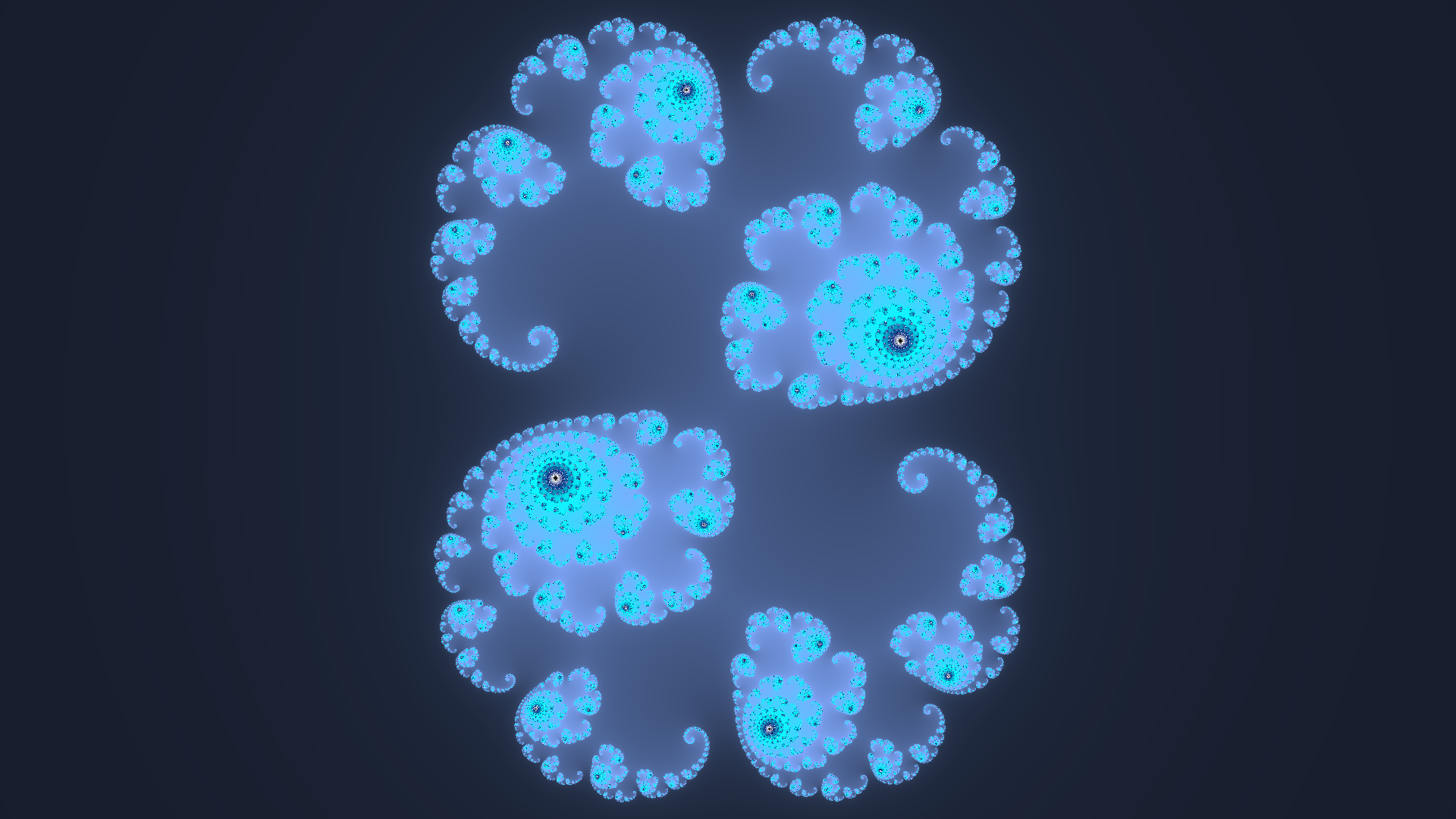
>>> Centrer(0.0, 0.0, 2.0)
>>> N_MAX = 500
>>> ORANGE = (255, 180, 60) ; VIOLET = (145, 40, 255)
>>> P = ConstruirePaletteDégradéMultiple(200, [NOIR, ORANGE, VIOLET, OUTREMER, BLEU, CYAN, BLANC])
>>>Julia_lisse(lambda z : z ** 2 - 0.8 + 0.156j, d = 2, Palette = P)
